This article may contain affiliate links. I will make a small commission if you make a purchase through one of these links, at no extra cost to you. This is how I hope to keep the website up and running for years to come! Please read my disclosure for more info.
“Make your money work for you” they say, but how? Compound interest is the answer you’re looking for! How does that work? That’s the topic of this article on one of the basics of personal finance – Let’s dive in!
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t, pays it.”
– Albert Einstein
Compound interest is your biggest frenemy
Frenemy, “a person who combines the characteristics of a friend and an enemy” that is what compound interest is. It can do wonders for you, but it sure can hurt you.
Let me illustrate this with the abbreviated story on wheat (or rice) and chessboard:
A ruler wanted to reward a man of humble origins with any reward of his choosing. The man responded with the request “Give me one grain of rice for the first square of the chessboard, two grains for the next square, four for the next, eight for the next and so on for all 64 squares, with each square having double the number of grains as the square before.” The ruler agreed, amazed that the man had asked for such a small reward – or so he thought. After a week, his treasurer came back and informed him that the reward would add up to an astronomical sum, far greater than all the rice that could conceivably be produced in many, many centuries!
To give you an idea of the reward the man asked for, the amount of grain on that last square would be 2^63 = 9,223,372,036,854,780,000.
It gets a bit trickier when you’re not starting at 1 or working with interest rates that aren’t 100%, but it translates to the following formula.
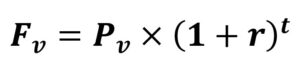
(where Fv = future value, Pv = present value, r = interest rate (%) and t = the number of times the interest rate is due)
Now turn this to money, and think about the interest or dividend received on investments, if added to the principal sum and reinvested it can in turn earn itself interest again, and again, and again. If, for example, Alex had 20,000 in the bank at 10% interest when Alex was 25 and left it there untouched until Alex was ready to retire at 65, Alex would have 905,185, if Alex had 23.000, Alex would retire a millionaire!
23,000 x (1 + 10%, or 1.10) ^45 = € 1,040,962.88
The longer you wait, the stronger it gets as you can see in the graph and table below. The growth is hardly noticeable in the beginning with only 10% and some change, but by the time Alex passes 50 the amount is growing more than 100% the original 23,000 per year, in the last year it earns quadrupple the original 23,000!
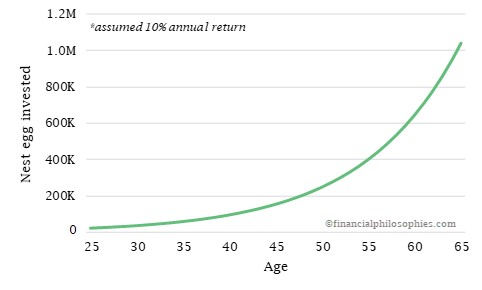
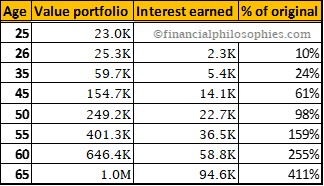
If you want so see the other side of your frenemy, take out a loan for 20,000 at a 17% interest rate, and don’t pay your dues, after 5 years this debt will have more than doubled to 43,848 (excl. fees or other costs). You’ll get now why it is important to be the one earning the interest, instead of paying it.
Rule of 72
An easier way to look at it is using a popular shortcut, the rule of 72, which tells you how many years it will take for an investment at a certain interest rate to double in value. The rule is (as depicted below) dividing 72 by the interest rate (the number, so 10% = 10 not 0.1); for example 72 divided by 10 means that with a 10% interest rate it will take 7.2 years for your investment to be doubled.
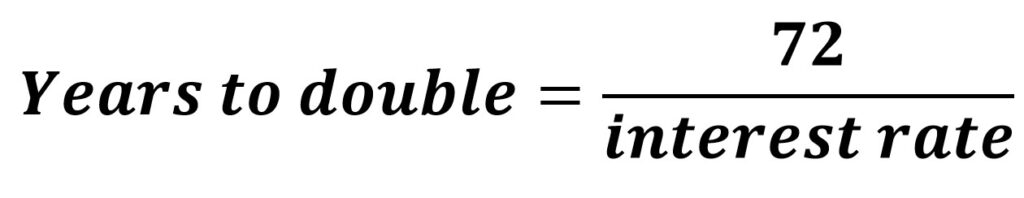
Side note: This formula is only applicable for annual compounding.
However, to get a more accurate result, resembling the first formula, it is best to use 69.3 instead of 72. Therefore, the rule of 69 should be more popular.
Final thoughts
The human mind isn’t great at comprehending the power of exponential growth, as the story of wheat (or rice) and chessboard illustrated. Therefore, it is even more important that you realize the power of compounding growth and how it can make or break you financial future.
Now I hope that you understand the wonders of compound interest and that you can earn it, instead of paying it! And remember to speed it up by continuously contributing, don’t let compounding do all the work (until later).
Want to have a compound interest calculator? Leave a message below and I can make that happen! Or perhaps you already have your favorite calculator, let me know below!
How useful was this post?
Click on a star to rate it!
Average rating 5 / 5. Vote count: 5
No votes so far! Be the first to rate this post.
We are sorry that this post was not useful for you!
Let us improve this post!
Tell us how we can improve this post?

